完全背包模板问题 - 凌冬的个人博客

完全背包问题

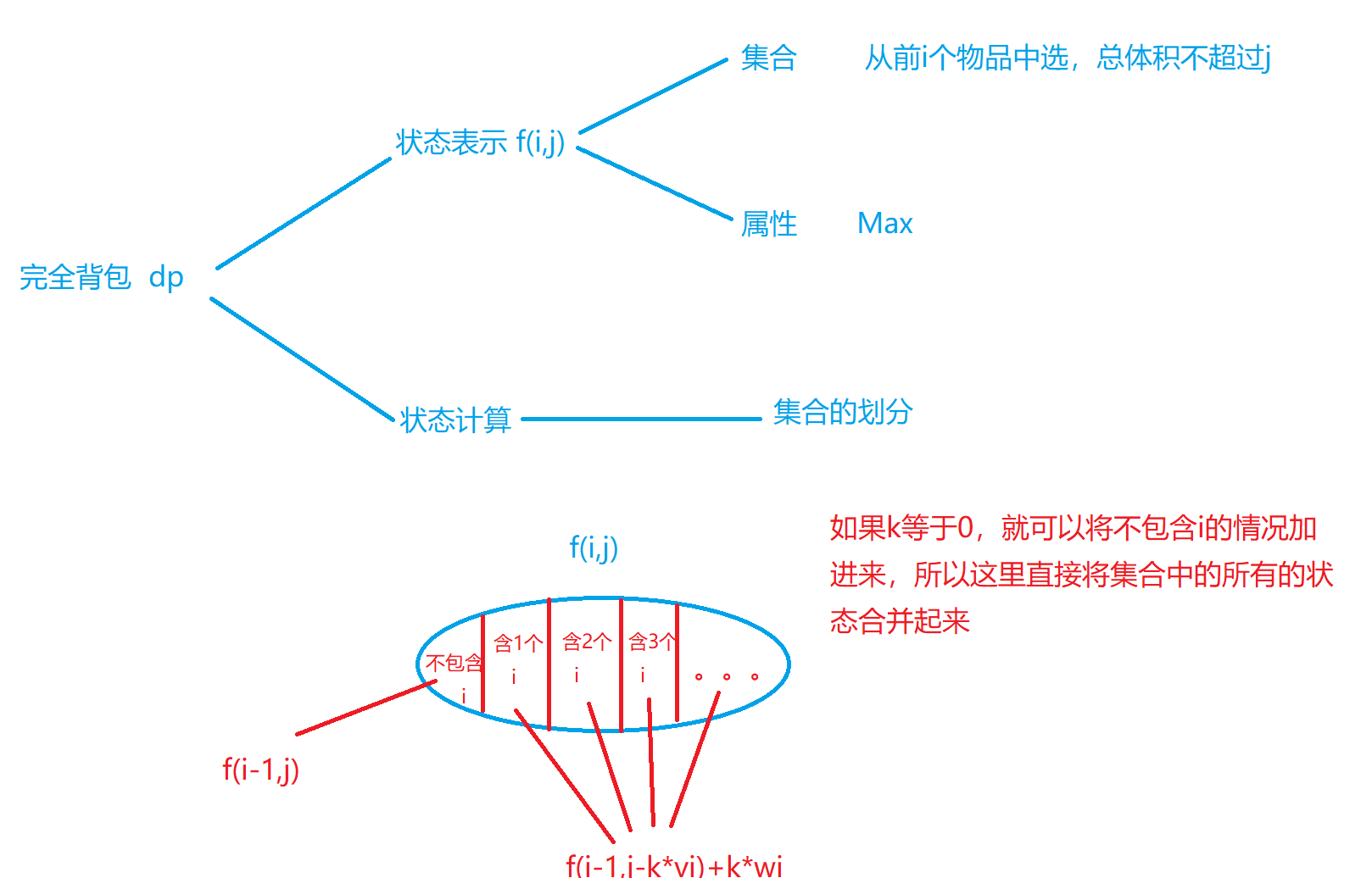
有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


#include <bits/stdc++.h>
using namespace std;
const int MAX = 3000;
int dp[MAX];
int n,m;
int main()
{
    
    cin>>n>>m;
    for (int i=0;i<n;i++) {
        int v,w;
        //体积，重量
        cin>> v>>w;
        for (int j=v;j<=m;j++) {
            //比较获得的最大值
            dp[j] = max(dp[j],dp[j-v] + w);
        }
    }
    cout << dp[m] <<endl;
    
    return 0;
}

一个正整数 n 可以表示成若干个正整数之和，形如：n=n1+n2+…+nk ，其中 n1≥n2≥…≥nk,k≥1

我们将这样的一种表示称为正整数 n 的一种划分。

现在给定一个正整数 n ，请你求出 n 共有多少种不同的划分方法。

输入格式

共一行，包含一个整数 n 。

输出格式

共一行，包含一个整数，表示总划分数量。

由于答案可能很大，输出结果请对 109+7 取模。

数据范围

1≤n≤1000

输入样例:

1

5

输出样例：

1

7

完全背包解法 状态表示： f[i][j]表示只从1~i中选，且总和等于j的方案数

状态转移方程: f[i][j] = f[i - 1][j] + f[i][j - i];

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
//最长上升子序列个数

const int mod = 1e9+7;
const int MAXN = 1010;
int dp[MAXN];

int main()
{
    int n;
    cin>>n;
    dp[0] = 1;
    //体积 是 n
    for (int i=1;i<=n;i++) {
        for (int j=i;j<=n;j++) {
            // 最大值 取max, 总和就 加法
            dp[j] = (dp[j] + dp[j-i]) % mod;
        }
    }
    cout << dp[n];
    
    return 0;
}