Difficulty: 困难
给定一个正整数 n,找出小于或等于 n 的非负整数中,其二进制表示不包含 **连续的1 **的个数。
示例 1:
1
2
3
4
5
6
7
8
9
10
11
|
输入: 5
输出: 5
解释:
下面是带有相应二进制表示的非负整数<= 5:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
其中,只有整数3违反规则(有两个连续的1),其他5个满足规则。
|
说明: $1<=n<=10^9$
解题公式推导:
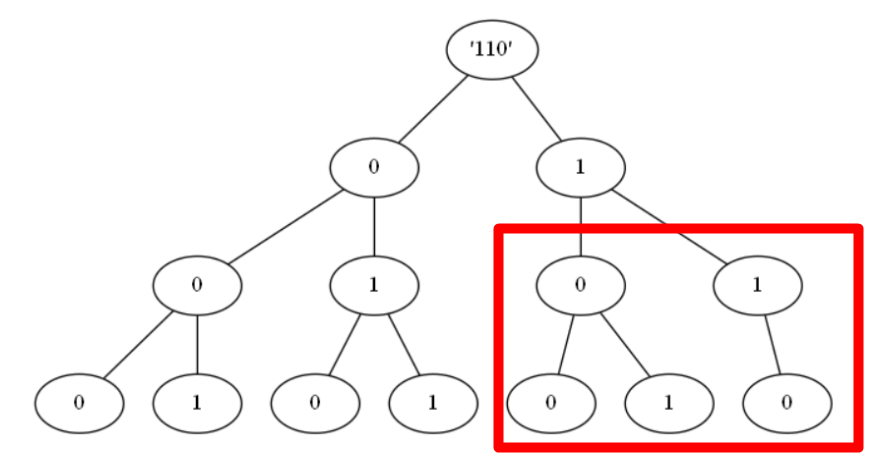
连续2个1 就不合法了,因此 我们 假设 所求值为 $dp[len][bit] $
数位DP 公式推导
$$ \begin{align} & dp[len][0] = (dp[len-1][1] + dp[len-1][0])\\ & dp[len][1] = dp[len-1][0] \end{align}$$
对 DP 公式的概括
$$
\begin{align} & dp[t] = \begin{cases} dp[t-1] + dp[t-2] , t>=2\\ 1,t<2
\end{cases}
\end{align}
$$
Solution
Language: ****
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
int findIntegers(int n) {
vector<int> v;
while(n) v.push_back(n%2),n/=2;
memset(dp,-1,sizeof dp);
return dfs(v,v.size()-1,0,1);
}
int dp[35][2];
int dfs(vector<int> &v,int pos,int pre,int limit) {
if(pos < 0) return 1;
if(!limit && dp[pos][pre] != -1)
return dp[pos][pre];
int cur = limit? v[pos]:1;
int res = 0;
for(int i=0;i<=cur;++i) {
if(i == 1 && pre == 1) continue;//连续2个1
res += dfs(v,pos-1,i,limit&&(i==cur) );
}
dp[pos][pre] = res;
return res;
}
};
|
非递归解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
int findIntegers(int n) {
vector<int> num;
while(n) num.push_back(n%2),n/=2;
vector<vector<int>> f(num.size() + 1, vector<int>(2));
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= num.size(); i ++ ) {
f[i][0] = f[i - 1][0] + f[i - 1][1];
f[i][1] = f[i - 1][0];
}
int res=0;
for(int i=num.size(),pre=0;i;--i) {
int t = num[i-1];
if(t) {
res += f[i][0];
if(pre) {
//当前位置不符合
return res ;
}
}
pre = t;
}
return res +1;
}
};
|

