1035. 不相交的线

Difficulty: ** 示例 2： 输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出：3 示例 3： 输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出：2 **

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

  • nums1[i] == nums2[j]
  • 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

1
2
3
4

输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

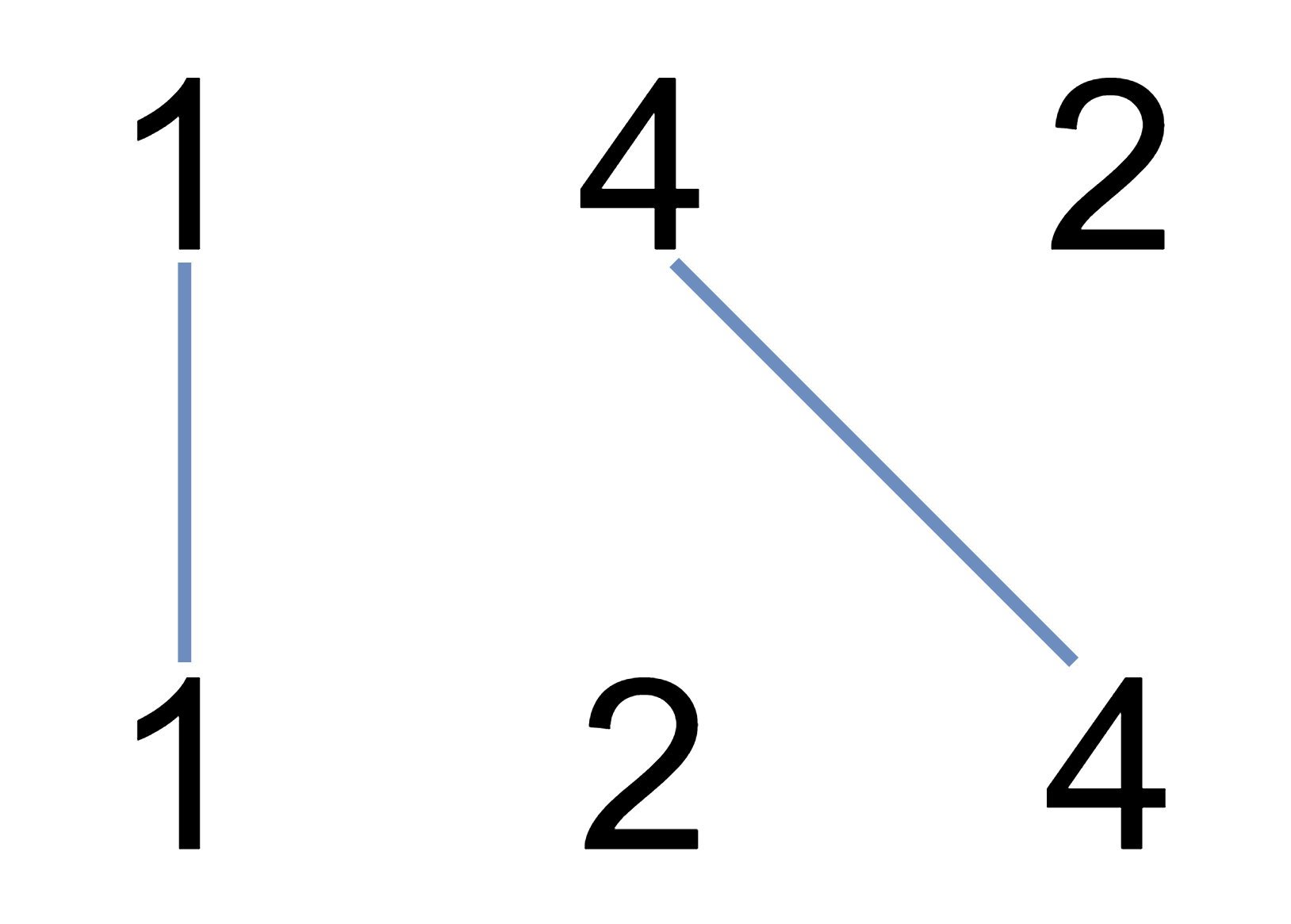
示例 2：

1
2

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

1
2

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

  • 1 <= nums1.length <= 500
  • 1 <= nums2.length <= 500
  • <font face="monospace" style="display: inline;">1 <= nums1[i], nums2[i] <= 2000</font>

Solution

解题思路分析

这是一道「最长公共子序列（LCS）」的轻度变形题。

为了让你更好的与「最长公共子序列（LCS）」裸题进行对比，

$$ dp[i,j]=\begin{cases}max(dp[i][j],dp[i-1][j-1] + 1),\quad &s[i]= p[j]\max(dp[i-1][j],dp[i][j-1]),\quad&s[i] \neq p[j]\end{cases} $$

Language: ****

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        //最长公共上升子序列变题
        int  n = nums1.size() , m = nums2.size();
        if ( n == 0 || m == 0) return 0;
        vector< vector<int>> dp(n+1,vector<int> (m+1));
        int ans = 0;
        for(int i=1 ;i<= n;++i) {
            for(int j=1;j<=m;++j) {
                if(nums1[i - 1] == nums2[j-1] ) {
                    dp[i][j] = max(dp[i][j] , dp[i-1][j-1] +1);
                    ans = max(ans, dp[i][j]);
                }else {
                    auto l1 = dp[i-1][j],
                         l2 = dp[i][j-1];
                    dp[i][j] = max(l1,l2);
                }
               
            }
            
        }
        return ans;

    }
};