硬币找零

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

你可以认为每种硬币的数量是无限的。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/gaM7Ch 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

动态规划原理

该算法为01背包问题

解题代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,99999);
        int n = coins.size();
        
        
        dp[0] = 0;
        for(int i=0;i<n;++i)
        {
            for(int j=coins[i];j<=amount;++j) {
                //如果选的话，硬币数+1， 如果不选的话，硬币数不变
                dp[j] = min( dp[j-coins[i]] + 1, dp[j] );
                //dp[j] 表示选出硬币数最少的
            }
            // for(int j=amount;j>=coins[i];--j) {
                //这个是01背包的解法，只能用1次
            //     dp[j] += dp[j-coins[i]];
            // }
        }
        return dp[amount] == 99999?-1:dp[amount];
    } 
};

递归原理

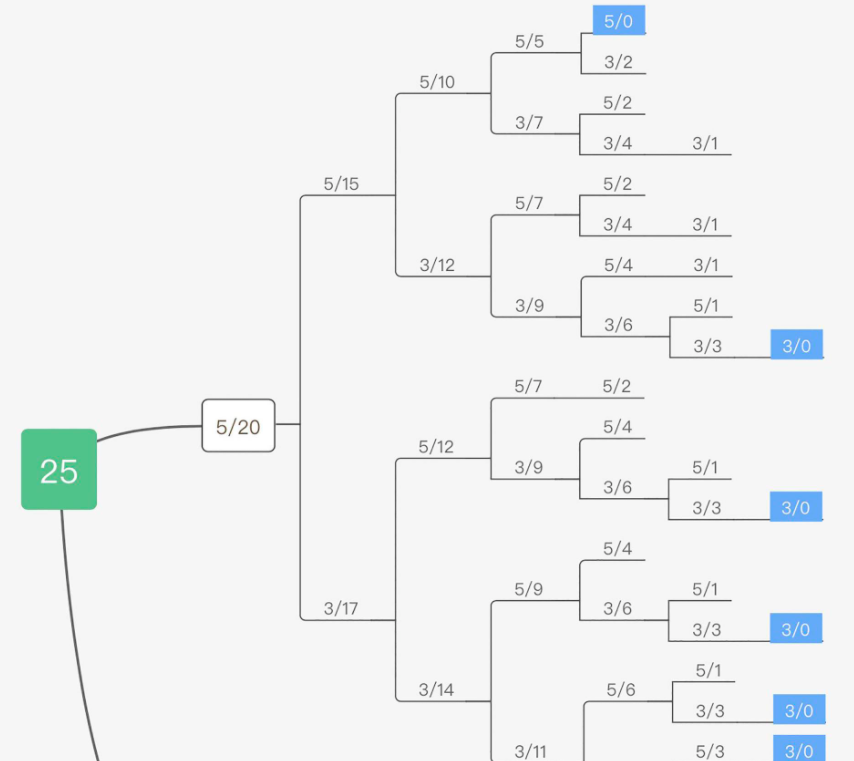
image-20210827122219109

于是 我们可以知道，层数越低，需要的硬币数量越少

动态规划求 min ，本质就是算出递归层数，然后取递归层数最小的那个方案 vector<int> dp(amount+1,INF);, 一开始假设所有方案都是 无穷大，然后 0 开始进行递归

解题代码【暴力搜索会超时】

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

const int INF = 9999999;
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int stack =  dfs(amount,coins);
        if (stack == INF) return -1;
        return stack;
    } 
    
    int dfs(int need, vector<int> &coins ) {
        if(need == 0) return 0;
        int stack = INF;
        for(int u: coins) {
            if(u> need) continue;
            if(u== need ) return 1;
            //u<need
            int level = dfs(need- u, coins);
            // if(level== INF ) continue;
            stack = min(stack, level+1);
        }

        return stack;
    }
};