lc.11.盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

输入：[1,8,6,2,5,4,8,3,7] 输出：49

解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1] 输出：1

提示：

n == height.length 2 <= n <= 105 0 <= height[i] <= 104

解题思路

如果没有真正理解题目，即使一次对着答案做出来了，再次遇到这个题目，还是可能做不出来。要理解这道题的正确性和原理，需要从背后的缩减搜索空间的思想去考虑题解

作者：nettee 链接：https://leetcode-cn.com/problems/container-with-most-water/solution/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/

解题代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.size() <=0) return 0;
        int l = 0,r = height.size()-1;
        int max_record = 0;
        while(l<r) {
            //if l==r return 0;
            int w = r-l;
            int h = min(height[l],height[r]);
            max_record = max(max_record,w*h);
            if(height[l] > height[r]) --r;
            else l++;//<= >靠拢
        }
        return max_record;
    }
};

实际上还有几道题也是用到了这样的缩减搜索空间的思想：

搜索状态图

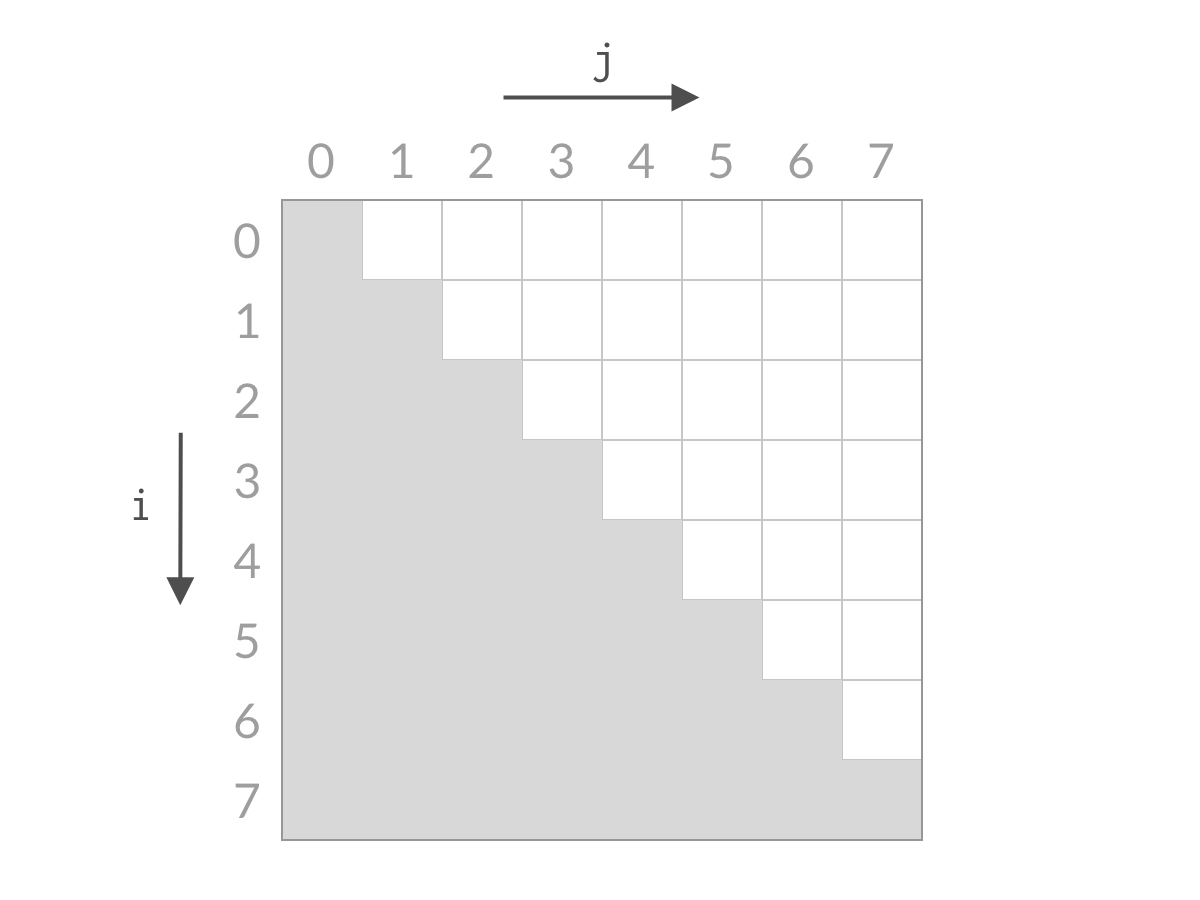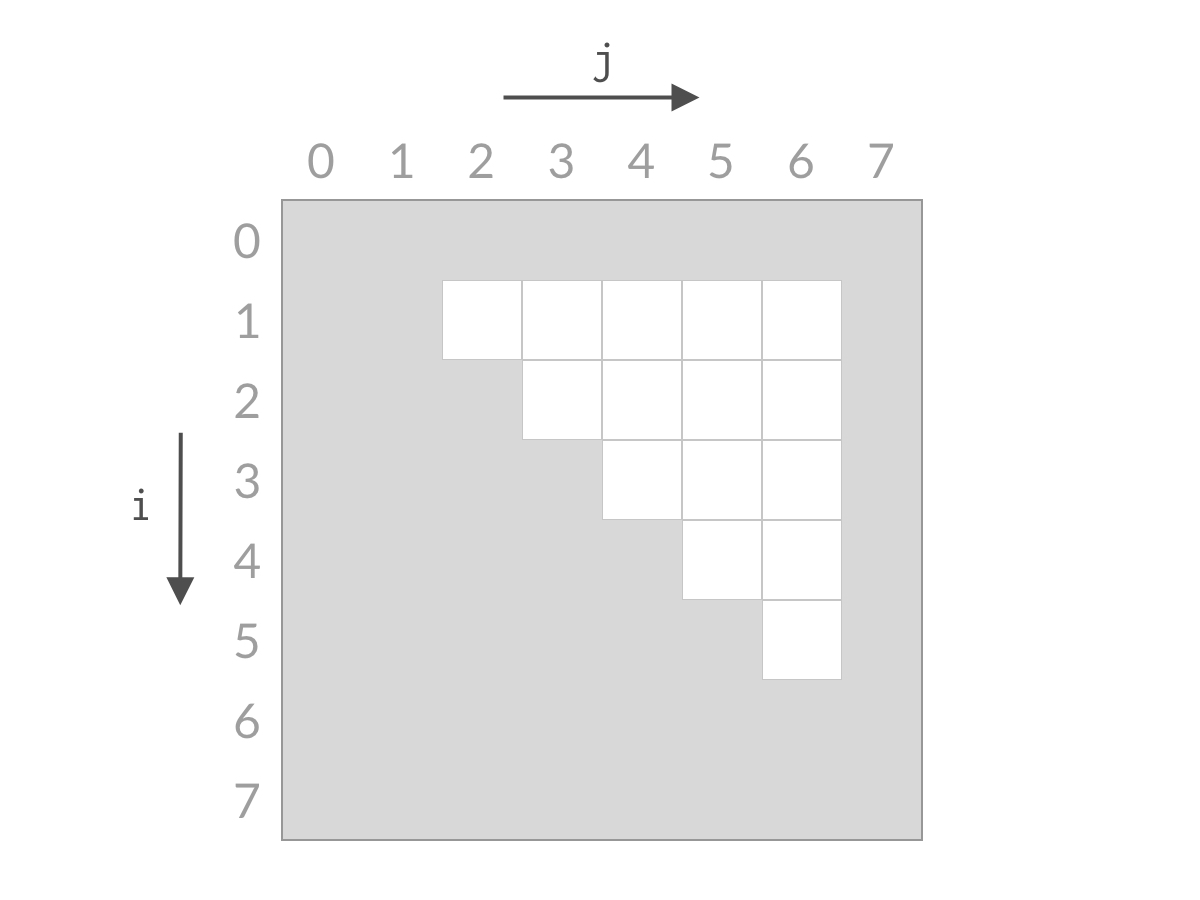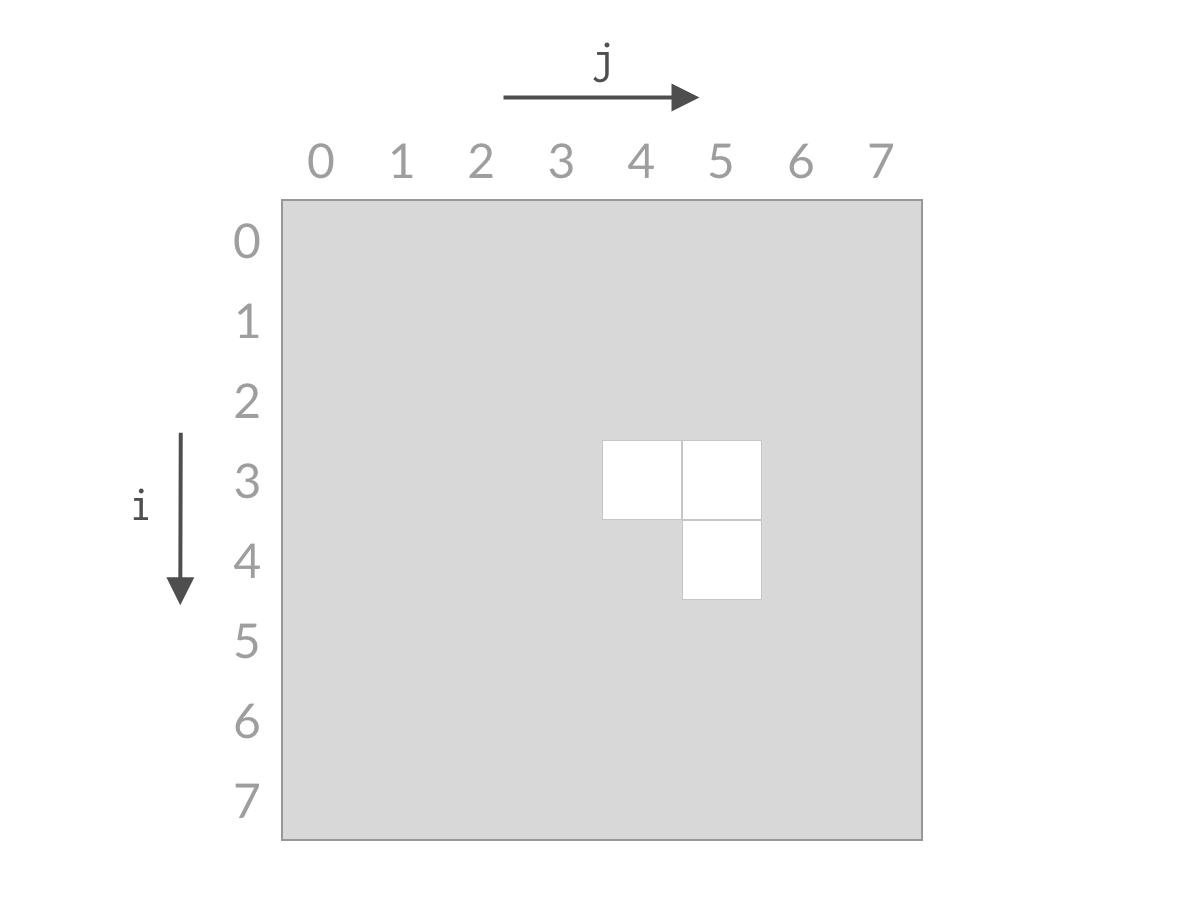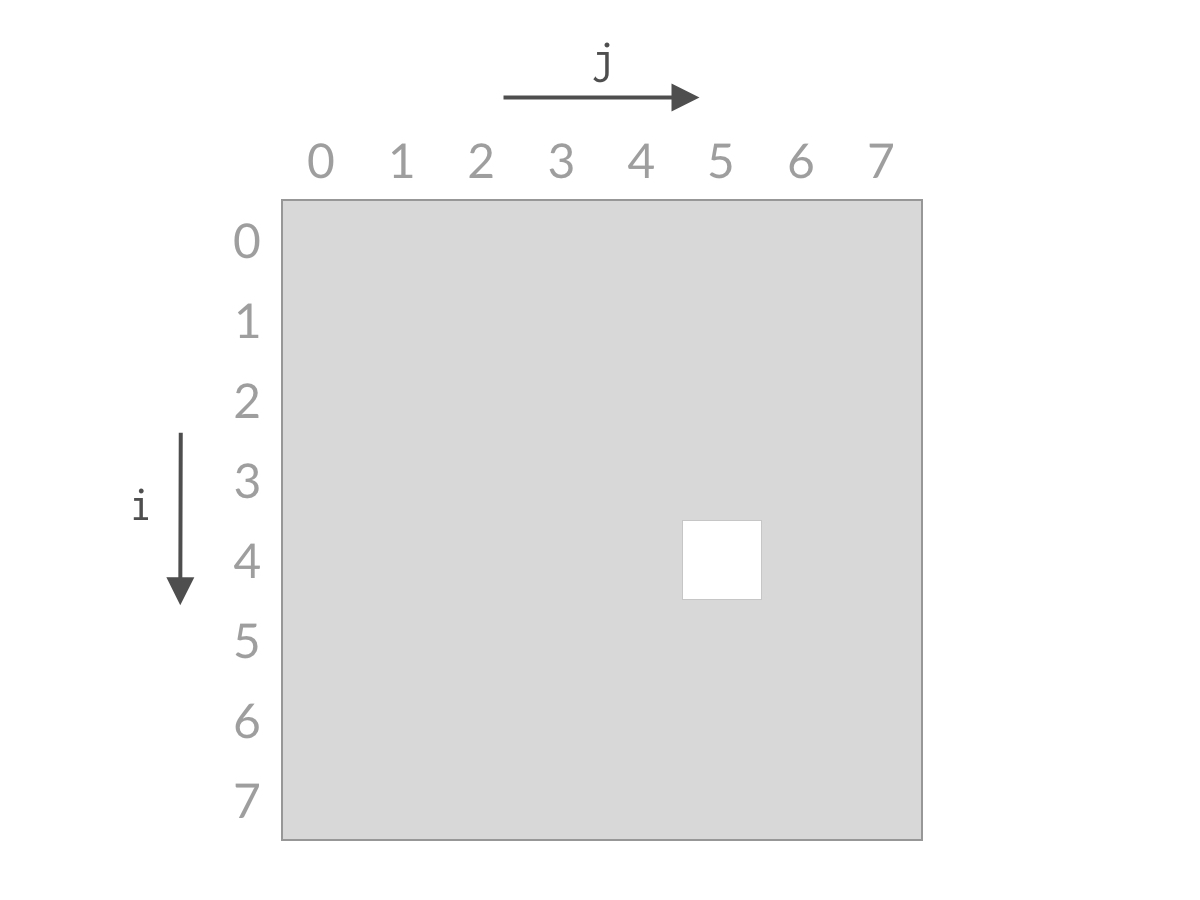
https://pic.leetcode-cn.com/9ebb3ff74f0706c3c350b7fb91fea343e54750eb5b6ae6a4a3493421a019922a.gif

240.搜索二维矩阵

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。每列的元素从上到下升序排列。

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出：true

示例 2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出：false

提示：

m == matrix.length n == matrix[i].length 1 <= n, m <= 300 -109 <= matrix[i][j] <= 109 每行的所有元素从左到右升序排列每列的所有元素从上到下升序排列 -109 <= target <= 109

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


/*
一个经典问题：给两个有序数组，要从中各选一个数，使两数之和为指定某个数。
如果把一个数组视为横轴，另一个数组视为纵轴，形成一张表格，格子里放「和」，那么就是这道题了。

*/ 

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& p, int target) {
        if(p.size()==0 || p[0].size()==0) return false;
        int col = p[0].size()-1,row = 0;
        int n = p.size();
        while(col>=0 && row < n) {
            if( p[row][col] ==target) return true;
            if( p[row][col] > target) --col;
            else ++row;
        }
        return false;
    }
};

文章目录