lc.167.两数之和II-有序数组

给你一个下标从 1 开始的整数数组 numbers ，该数组已按非递减顺序排列，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9 输出：[1,2] 解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6 输出：[1,3] 解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1 输出：[1,2] 解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

提示：

2 <= numbers.length <= 3 * 104 -1000 <= numbers[i] <= 1000 numbers 按非递减顺序排列 -1000 <= target <= 1000 仅存在一个有效答案

思路

双指针本质：相等于杨氏矩阵，而杨氏矩阵又相等于有序集合的笛卡尔积。右上角的数字就等于原序列的第一个值加上最后一个值，而我们向下走一步就意味着 left 向后移动一位，这刚好就是当前位置小于 target 的情况。同理，向左走一步就意味着 right 向前移动一步，也就是当前位置大于 target 的情况。

双指针图文解释

而我们希望从中找到满足 A[i] + A[j] == target 的下标 (i, j) 。以 n=8 为例，这时候全部的搜索空间是：如图白色三角

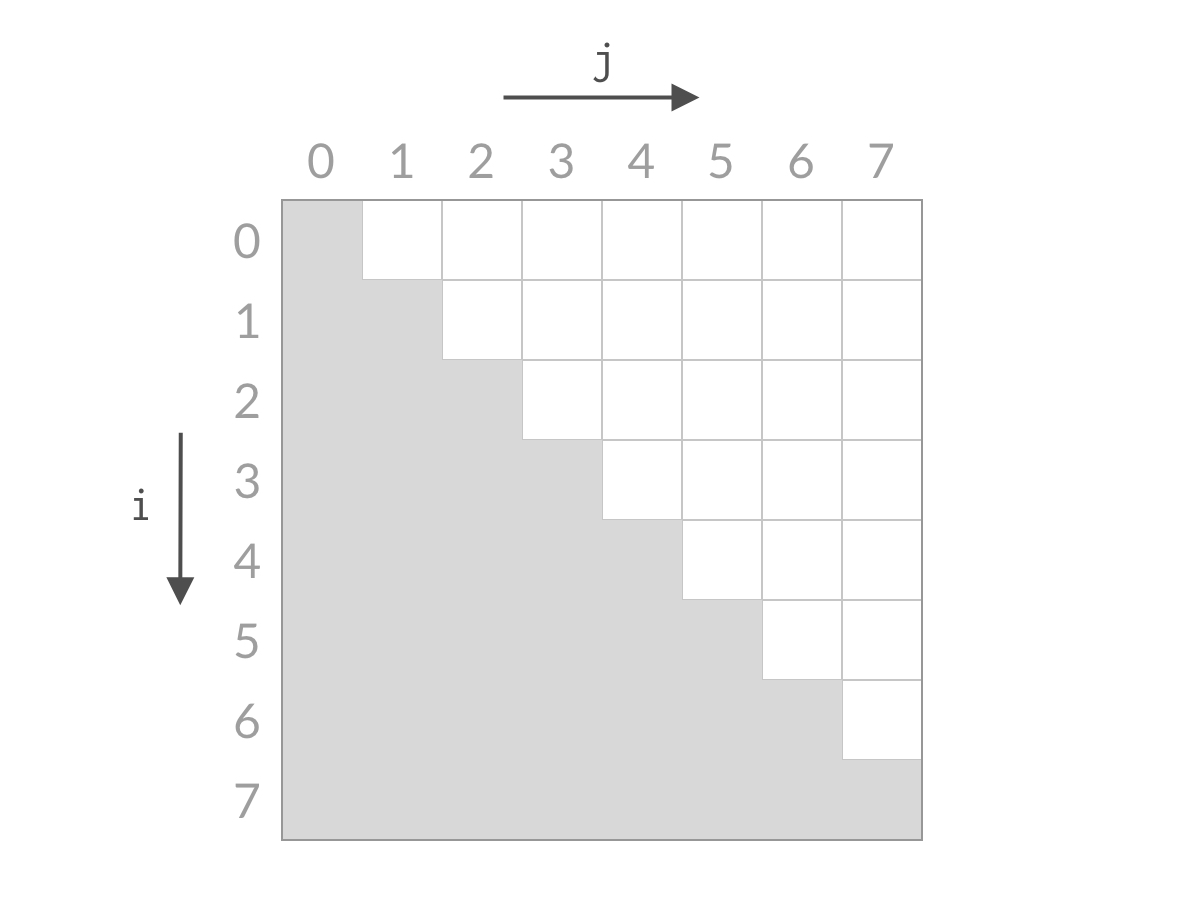
https://pic.leetcode-cn.com/6ee3750f6036a7a6249197e5b640bfc0564153ca1a61c1e35aad51f3a8f9dc5e.jpg

搜索的过程如下

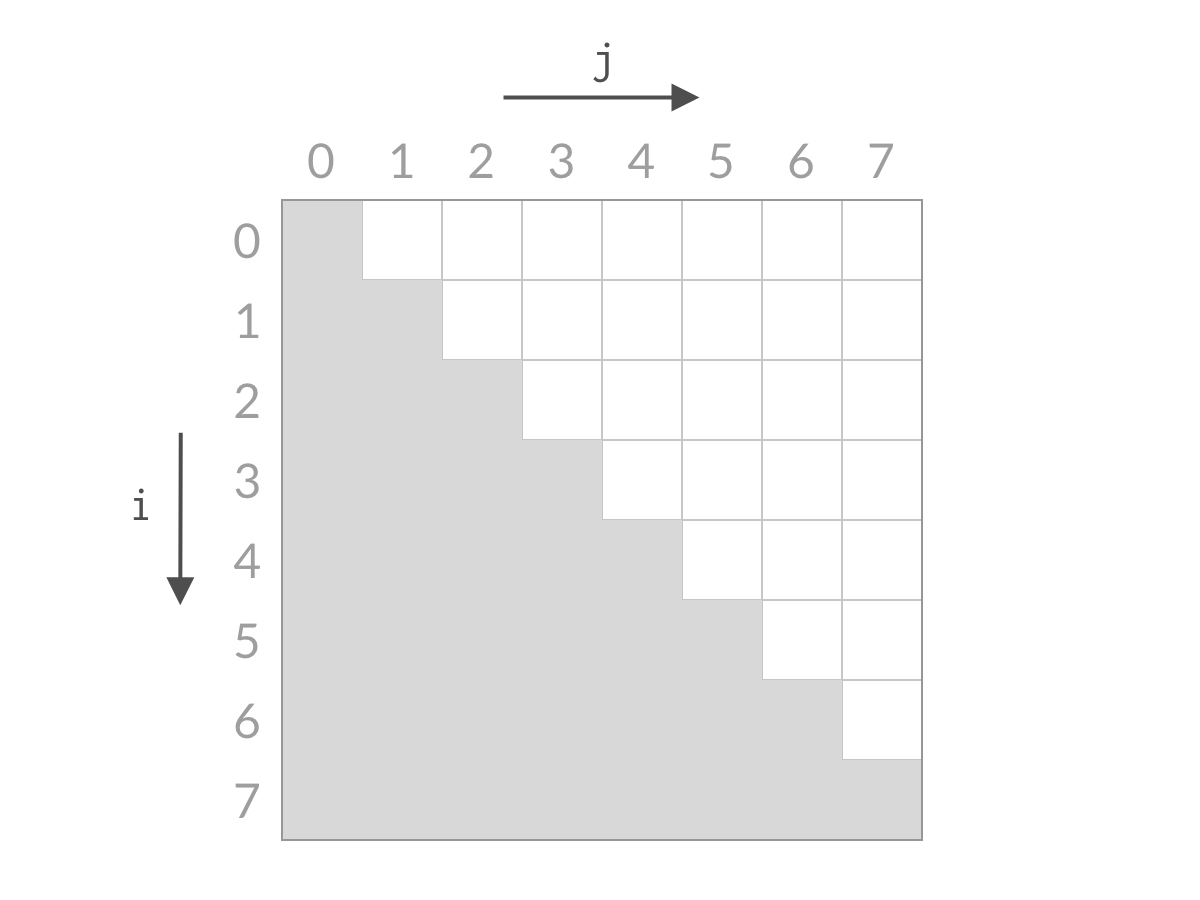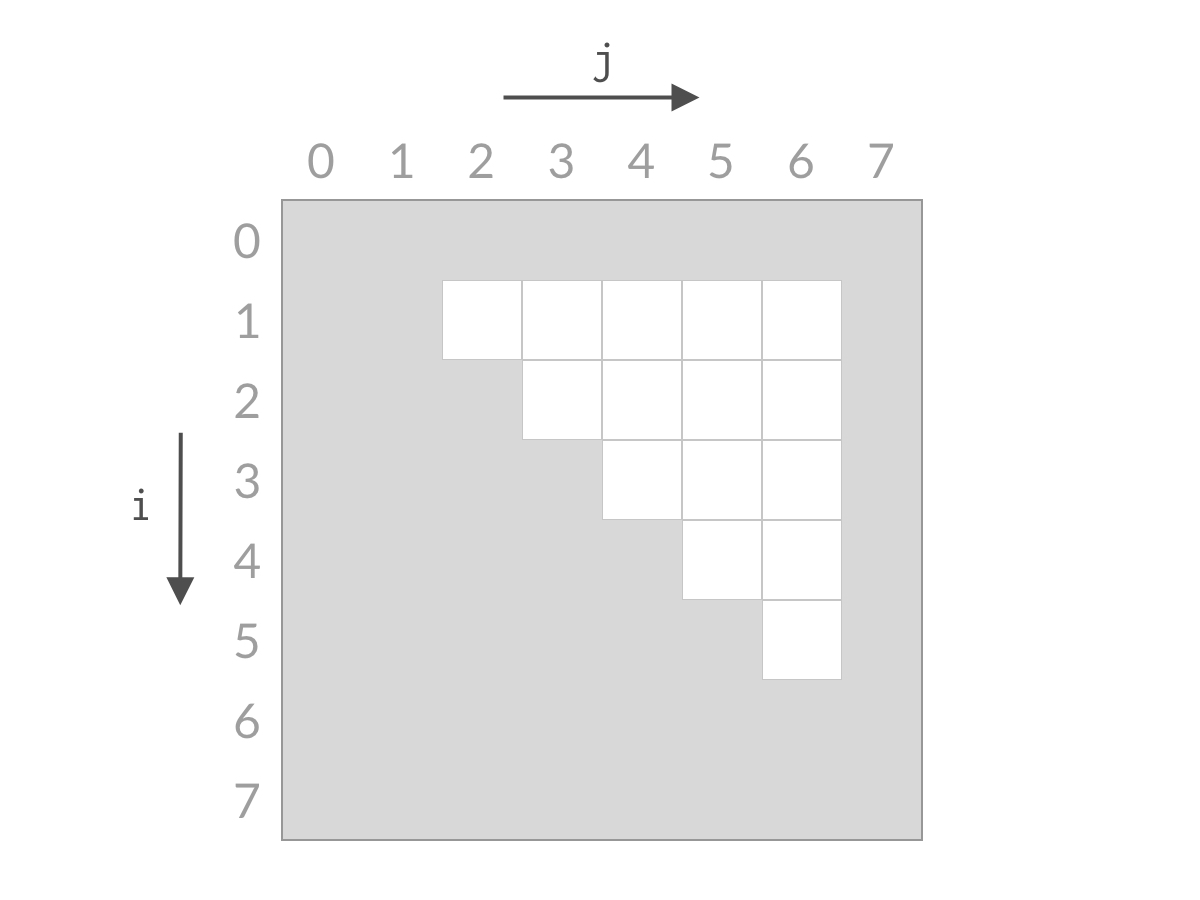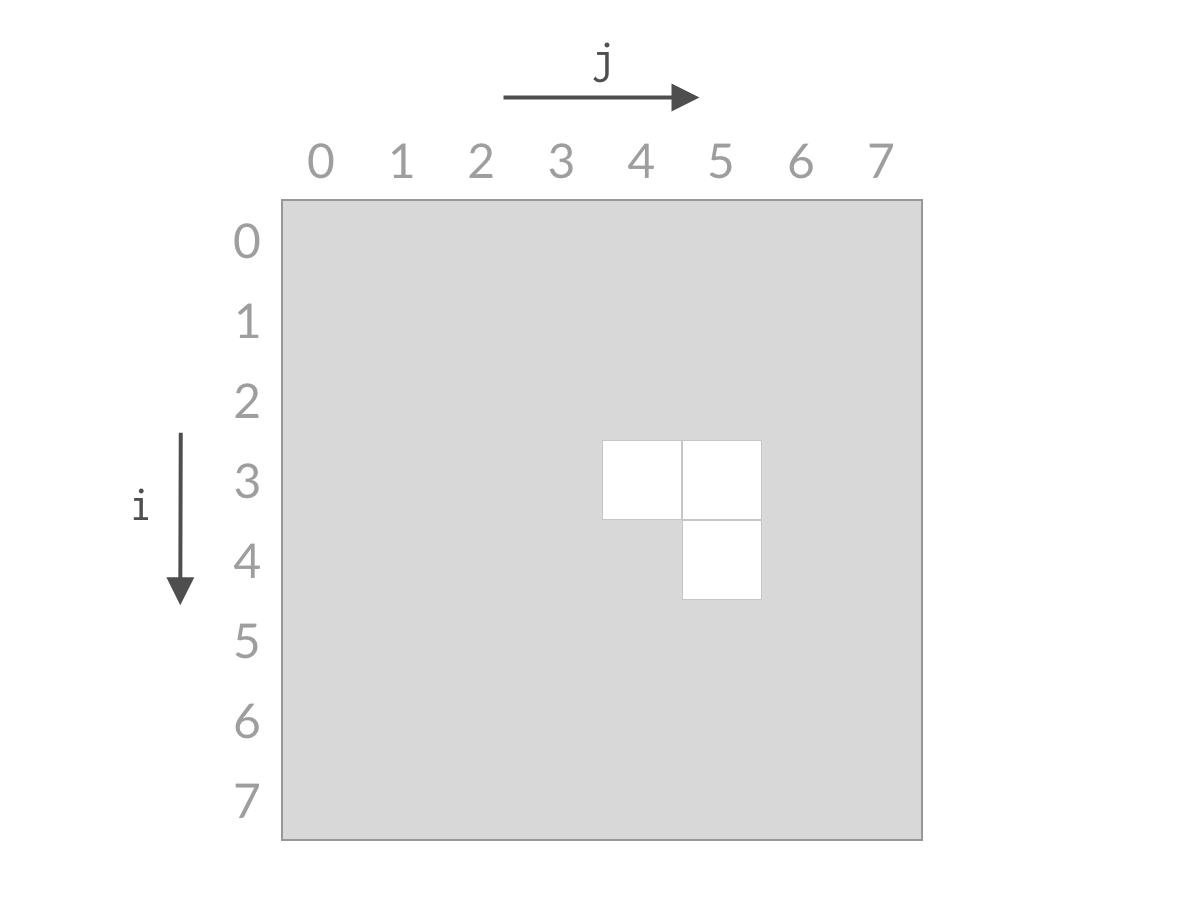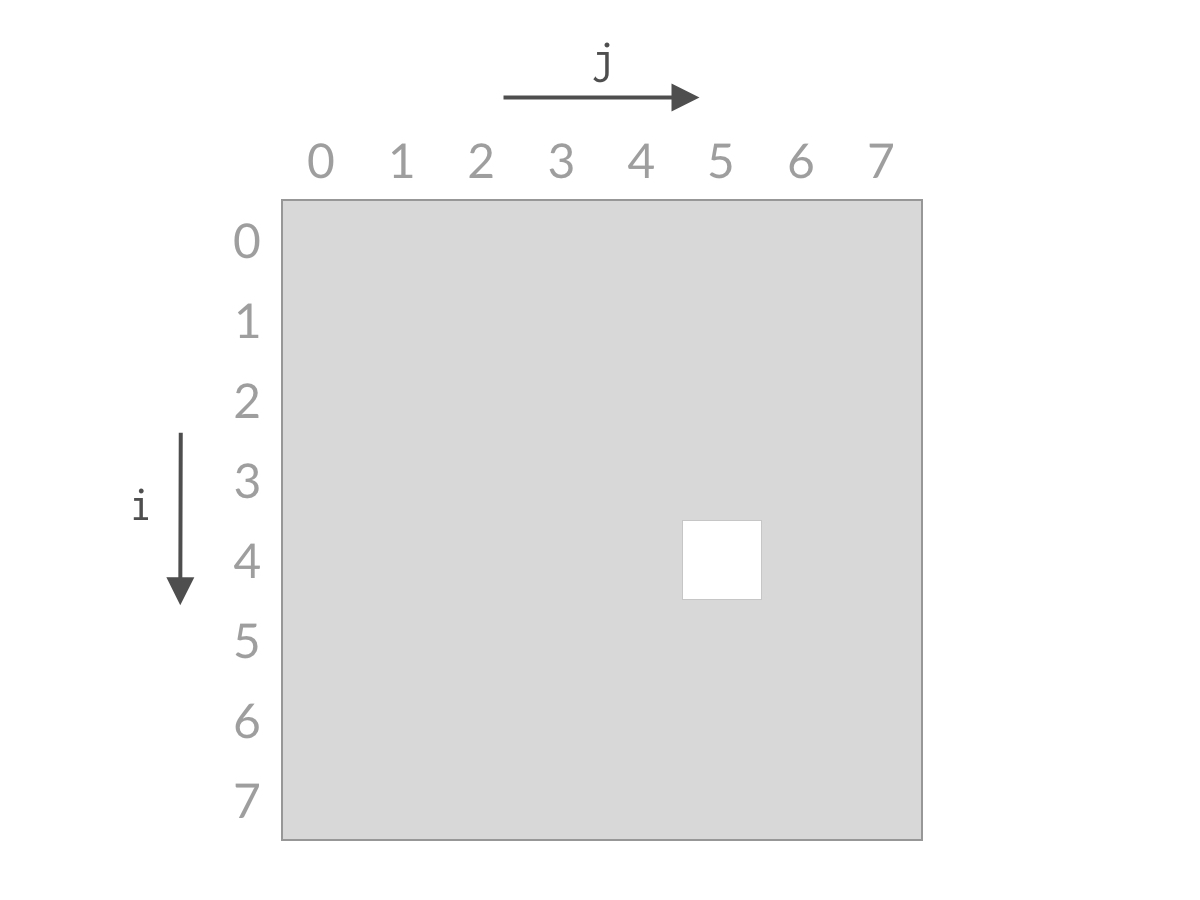
https://pic.leetcode-cn.com/9ebb3ff74f0706c3c350b7fb91fea343e54750eb5b6ae6a4a3493421a019922a.gif

j从右往左，i从上往下，最后搜索范围不断缩小

类似的问题可以看 leetcode.240.搜索二维矩阵

一个经典问题：给两个有序数组，要从中各选一个数，使两数之和为指定某个数。

如果把一个数组视为横轴，另一个数组视为纵轴，形成一张表格，格子里放「和」，那么就是这道题了。

解题思路

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


 
class Solution {
public:
    vector<int> twoSum(vector<int>& a, int target) {
        if(a.size()<2) return {};
        int l=0,r = a.size()-1;
        vector<int> res(2);
        while(l<r ) {
            int x = a[l],y = a[r];
            if(x+y > target) {
                --r;
            }else if(x+y<target) {
                ++l;
            }else {
                res[0] = l+1;
                res[1] = r+1;
                // ++l;
                break;
            }
        }

        return res;
    }
};

双指针算法

时间复杂度是 $o(nlogn)$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
public:
    
    vector<int> twoSum(vector<int>& a, int target) {
        if(a.size()<2) return {};
        
        int n = a.size();
        for(int i=0;i<n;i++) {
            int l = i+1,r = a.size()-1;
             // a[i] + a[j] == target 
             while(l<=r) {
                 int mid = l+ (r-l)/2;
                 //a[j]
                 int aj = a[mid];
                 if(a[i]   < target -aj) {//target -aj
                    l = mid+1;
                 }else if(a[i]  > target -aj) {
                     r = mid-1;
                 }else {
                     
                     if(mid < i) {
                         swap(i,mid);
                     }
                     return {i+1,mid+1};
                 }
             }

        }
        return {};

      
    }
};

文章目录