强连通分量_受欢迎的牛 - 凌冬的个人博客

每一头牛的愿望就是变成一头最受欢迎的牛。

现在有 N 头牛，编号从 1 到 N ，给你 M 对整数 (A,B) ，表示牛 A 认为牛 B 受欢迎。

这种关系是具有传递性的，如果 A 认为 B 受欢迎， B 认为 C 受欢迎，那么牛 A 也认为牛 C 受欢迎。

你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。

输入格式

第一行两个数 N,M

接下来 M 行，每行两个数 A,B ，意思是 A 认为 B 是受欢迎的（给出的信息有可能重复，即有可能出现多个 A,B ）。

输出格式

输出被除自己之外的所有牛认为是受欢迎的牛的数量。

数据范围

$ 1≤N≤10^4 $ $ 1≤M≤5×10^4 $

输入样例：

输出样例：

1

1

样例解释

只有第三头牛被除自己之外的所有牛认为是受欢迎的

解题思路

dfn[u]dfs遍历到u的时间(如上图中的数字) low[u]从u开始走所能遍历到的最小时间戳(上图中1,2,3,4,5都是一个环/强连通分量中的即dfn[1]=low[1]=low[2]=low[3]=low[4]=low[5]) –即u如果在强连通分量,其所指向的层数最高的点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


inline int tarjan(int u) 
{
    low[u]=dfn[u]=++dfn_sum;
    stack[top++]=u;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(dfn(v))
            low[u]=min(low[u],dfn[v]);
        else
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
    }
    if(low[u]==dfn[u])
    {
        int now=stack[--top];s_sum++;
        s[u]+=s_sum;
        while(now!=u)
        {
            s[now]=s_num;
            now=s[--top];
        }
    }
}

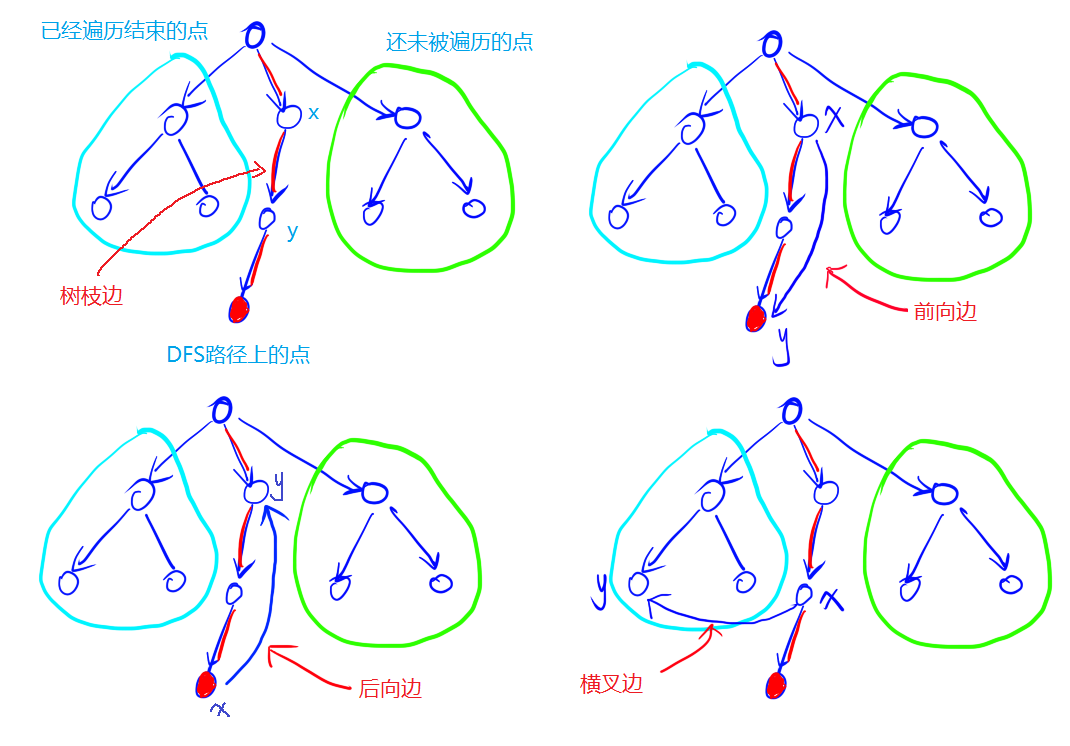
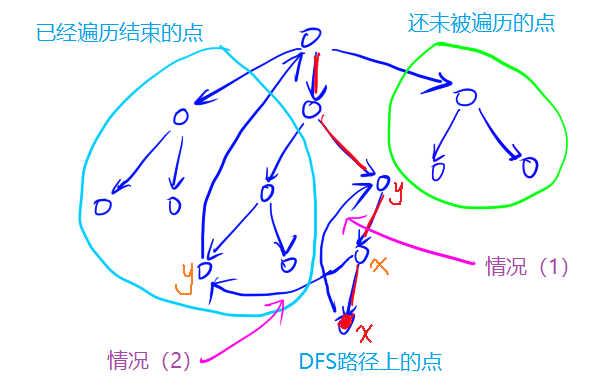
对每个点定义两个时间戳： dfn[u] 表示遍历到的 u 的时间戳。 low[u] 从 u 开始走，所能遍历到的最小时间戳是什么。如果 u 是其所在的强联通分量的最高点，等价于$ dfn[u] == low[u] $

解题代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82


#include<bits/stdc++.h>
using namespace std;
const int MAXN = 10010;
#define next NEXT
 
int inStk[MAXN];
int stk[MAXN],top;
int n,m;
int flag;
int dfn[MAXN] , low[MAXN];
int scc_cnt;
int id[MAXN],Size[MAXN];
int dout[MAXN];
unordered_map<int,vector<int>> path;
void tarjan(int u) {
    dfn[u] = low[u] = ++ flag;
    stk[++top] = u;
    inStk[u] = 1;
     
    for(auto next: path[u]) 
    {
        if(!dfn[next]) {
            tarjan(next);
            //回溯到了这个点，直接更新
            low[u] = min(low[u],low[next]);
        }else if (inStk[next]) {
            //正在 stack 中，还没有被回溯
            //相当于 2图中的 y -> root
            low[u] = min(low[u],dfn[next]);
        }
    }
    if(dfn[u] == low[u]) {
        //无法再搜索其他节点，回溯
        ++scc_cnt;
        int tt;
        do {
            tt = stk[top--];
            inStk[tt ] = false;
            id[tt] = scc_cnt;
            ++Size[scc_cnt];
        }while(tt != u);
    }
}



int main()
{
    cin>> n>>m;
    while(m --) {
        int u,v;
        cin>>u >>v;
        path[u].push_back(v);
    }
    for(int i=1;i<=n;++i)
        if(!dfn[i])
            tarjan(i);
    for(int i=1;i<=n;++i) {
        for(int next: path[i]) {
            int a = id[i],
                b = id[next];
            //printf("%d , %d\n",a,b);;
            if(a != b) dout[a]++;// a!=b
        }
    }
    int zeros= 0,sum =0;
    for(int i=1;i<=scc_cnt;++ i) {
        if(dout[i] == 0) {
            zeros++;
            sum += Size[i];
            //printf("--- %d\n", sum);
            if(zeros> 1) {
                //出现多个出点，
                //出度为 0 的点 只能有1个
                sum  = 0;
                break;
            }
        }
    }
    printf("%d\n",sum);
    return 0;
}

文章目录