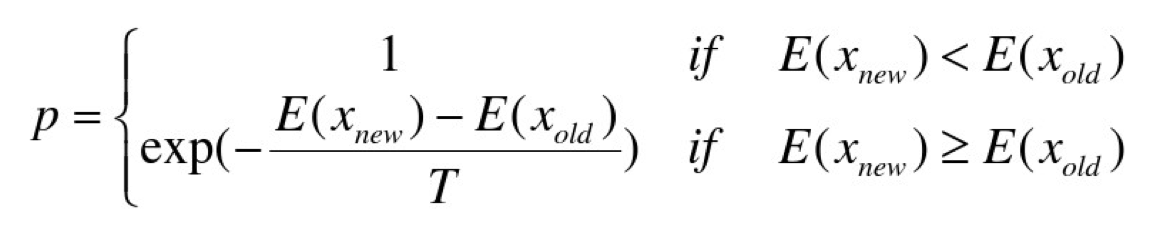模拟退火算法 - 凌冬的个人博客

模拟退火算法入门

介绍模拟退火前，先介绍爬山算法。爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。

爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如图1所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。

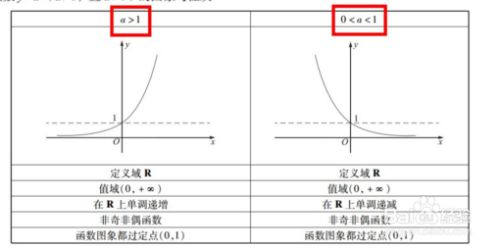
模拟退火算法的核心思想与热力学的原理极为相似，在高温下，液体的大量分子彼此之间进行相对移动，如果液体慢慢冷却，原子的可动性就会消失，原子自行排列成行，形成一个纯净的晶体．如果温度冷却迅速，那它不一定能达到这个状态，这一个过程的本质在于，慢慢冷却，使原子在丧失可动性之前重新排列，达到低能状态的必要条件．

模拟退火算法的描述：

模拟退火公式

$f(new_pos) - f(cur_pos) = \Delta{E}$

参考视频

e的x次方怎么得0

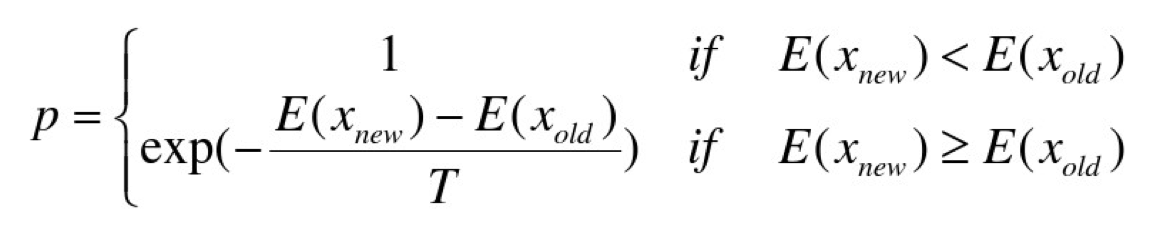
例题

在二维平面上有 n 个点，第 i 个点的坐标为 (xi,yi)。

请你找出一个点，使得该点到这 n 个点的距离之和最小。

该点可以选择在平面中的任意位置，甚至与这 n 个点的位置重合。

输入格式

第一行包含一个整数 n。

接下来 n 行，每行包含两个整数 xi,yi ，表示其中一个点的位置坐标。

输出格式

输出最小距离和，答案四舍五入取整。

数据范围

1
2


1≤n≤100 ,
0≤xi,yi≤10000 

输入样例：

1
2
3
4
5


4
0 0
0 10000
10000 10000
10000 0

输出样例：

1

28284

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50


#include<bits/stdc++.h>
using namespace std;

const int MAXN = 110;
struct Point{
  double x,y;  
} p[MAXN];

int n;
double ans = 1e9;
double dist(Point &a ,Point &b) {
    double x = a.x - b.x, y = a.y - b.y;
    return sqrt(x*x + y *y);
}


double calc(Point t) {
    double sum = 0;
    for(int i=0;i<n;++i) 
        sum += dist(t, p[i]);
    ans = min(ans,sum);
    return sum;
}
double rand(double l,double r) {
    return (double)rand()/RAND_MAX * (r-l) + l;
}

void ac() {
    Point cur= {rand(0,10000),rand(0,10000)};
    
    for(double T = 1e4;T>1e-4;T*=0.99) {
        Point t = { rand(cur.x-T,cur.x + T), rand(cur.y-T,cur.y+T)  };
        double pk = calc(t) - calc(cur);
        if(exp(-pk/T) > rand(0,1)) {
            cur = t;
        }
    }
}

int main(void) {
    
    srand(time(0));
    scanf("%d", &n);
    for(int i=0;i<n;i++)
        scanf("%lf%lf", &p[i].x, &p[i].y);
    for(int i=0;i<100;i++) ac();
    printf("%.0lf\n",ans);
    
    return 0;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53


#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <ctime>
#define x first
#define PDD pair<double,double>
#define y second
using namespace std;
const int N = 110;
typedef double ff;
int n;
PDD q[N];

ff ans = 1e18;

ff dist(PDD a,PDD b ) {
    ff dx = a.x - b.x;
    ff dy = a.y - b.y;
    return sqrt(dx*dx + dy * dy);
}

ff rand(ff l, ff r) {
    return (ff) rand()/RAND_MAX*(r - l) + l;
}

ff calc(PDD p) {
    ff res = 0;
    for (int i  =0; i < n; i ++ ) 
        res += dist(p,q[i]);
    ans = min(ans, res);
    return res;
}

void firedown() {
    PDD cur(rand(0,10000),rand(0,10000));//随机一个初始点
    for (ff t = 1e4; t > 1e-4; t *= 0.99) {//初始值（步长），终止值，衰减系数
        PDD newpoint(rand(cur.x - t,cur.x + t), rand(cur.y - t, cur.y + t));//在当前点周围随机一个新点
        ff dt = calc(newpoint) - calc(cur);
        if (exp(-dt/t) > rand(0,1)) cur = newpoint;
        //如果比当前好就跳过去
        //否则以一定概率跳过去
    }
}

int main () {
    cin >> n;
    for  (int i  = 0; i <n ; i ++ ) cin >> q[i].x >> q[i].y;
    for (int  i = 0; i< 100; i ++ ) firedown();
    printf("%.0lf\n",ans);
}
 

文章目录

模拟退火算法 入门