八大排序以及java实现

插入排序

算法描述

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


public int[] sort(int[] nums) {
  int len = nums.length;
  for(int i = 1; i < len; i++) {
    int n = nums[i];
    for(int j = i; j>0 && n<nums[j-1]; j--) {
			nums[j] = nums[j-1];
    }
    nums[j] = n;
  }
  return nums;
}

直接插入排序复杂度如下：

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(n²)	O(n²)	O(n²)	O(1)	稳定

选择排序

算法描述

从未排序序列中，找到关键字最小的元素
如果最小元素不是未排序序列的第一个元素，将其和未排序序列第一个元素互换
重复1、2步，直到排序结束。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


public int[] sort(int[] nums) {
    int len = nums.length;
        for(int i = 0; i < len; i++) {
            int min = i;
            for(int j = i + 1; j < len; j++) {
                    if(nums[j] < nums[min]) {
                        min = j;
                    }
            }
            int tmp = nums[i];
            nums[i] = nums[min];
            nums[min] = tmp;
        }
        return nums;
}

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(n²)	O(n²)	O(n²)	O(1)	不稳定

冒泡排序

算法描述

冒泡排序算法的运作如下：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


public int[] sortArray(int[] nums) {
        int len = nums.length;
        for(int i = 0; i < len; i++) {
            for(int j = 0; j < len-i-1; j++) {
                    if(nums[j] > nums[j+1]) {
                        int tmp = nums[j];
                        nums[j] = nums[j+1];
                        nums[j+1] = tmp;
                    }
            }
        }
        return nums;
    }

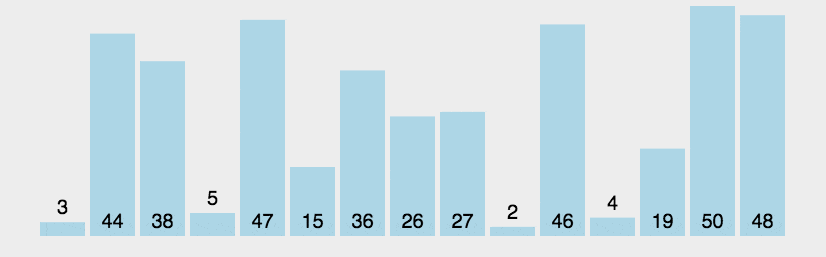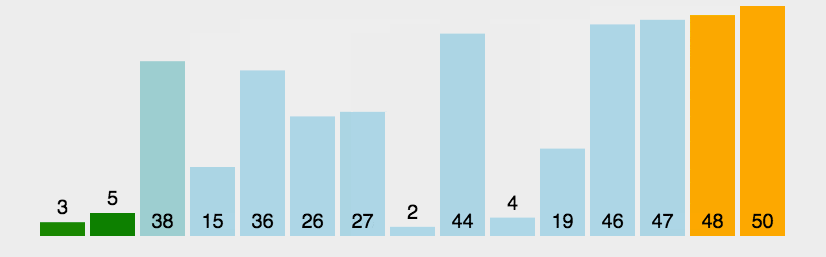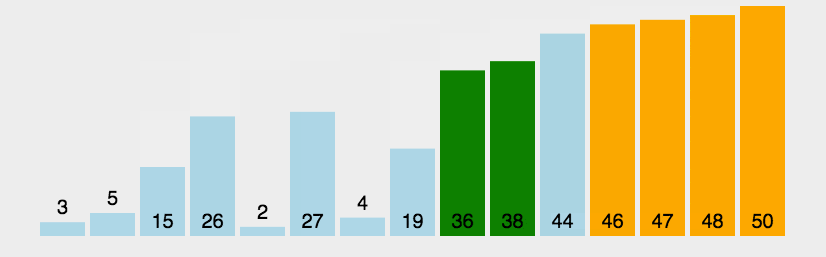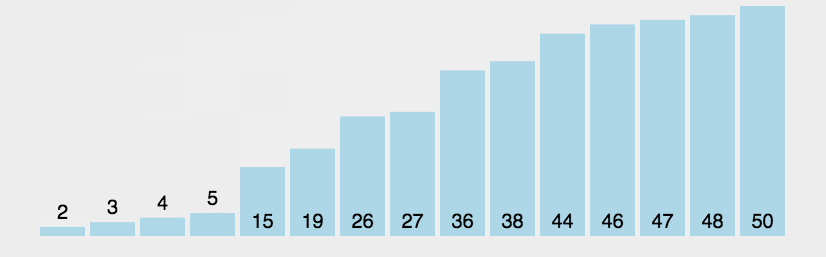
改进的冒泡排序最好情况可以做到O(n)，就是遍历了一次发现全部有序，则无需在多几轮了

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(n²)	O(n)	O(n²)	O(1)	稳定

快速排序

算法描述

快速排序使用分治策略来把一个序列（list）分为两个子序列（sub-lists）。步骤为：

从数列中挑出一个元素，称为"基准"（pivot）。
重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


public void fastSort(int[] a, int lo, int hi) {
        if (lo >= hi) {
            return;
        }
        int left = lo;
        int right = hi;

        //保存基准值
        int pivot = a[left];
        while (left < right) {
            //从后向前找到比基准小的元素
            while (left < right && a[right] >= pivot)
                right--;
            a[left] = a[right];
            //从前往后找到比基准大的元素
            while (left < right && a[left] <= pivot)
                left++;
            a[right] = a[left];
        }
        // 放置基准值，准备分治递归快排
        a[left] = pivot;
        fastSort(a, lo, left - 1);
        fastSort(a, left + 1, hi);
    }

以下是快速排序算法复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(nlog₂n)	O(nlog₂n)	O(n²)	O(1)	不稳定

归并排序

算法描述

将序列每相邻两个数字进行归并操作，形成 floor(n/2)个序列，排序后每个序列包含两个元素；
将上述序列再次归并，形成 floor(n/4)个序列，每个序列包含四个元素；
重复步骤2，直到所有元素排序完毕。

以下是归并排序算法复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(nlog₂n)	O(nlog₂n)	O(nlog₂n)	O(n)	稳定

堆排序

算法描述

先将初始序列𝐾[1..𝑛]建成一个大顶堆, 那么此时第一个元素𝐾1最大, 此堆为初始的无序区.
再将关键字最大的记录𝐾1 (即堆顶, 第一个元素)和无序区的最后一个记录 𝐾𝑛 交换, 由此得到新的无序区𝐾[1..𝑛−1]和有序区𝐾[𝑛], 且满足𝐾[1..𝑛−1].𝑘𝑒𝑦𝑠⩽𝐾[𝑛].𝑘𝑒𝑦
交换𝐾1 和 𝐾𝑛 后, 堆顶可能违反堆性质, 因此需将𝐾[1..𝑛−1]调整为堆. 然后重复步骤2, 直到无序区只有一个元素时停止。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


public int[] sortArray(int[] nums) {
  for(int i = nums.length-1; i>0;i--) {
    // 每次都重新构建一次堆
    max_heapify(nums, i);

    // 将堆顶放到最后，表示已经确定排序了
    int tmp = nums[0];
    nums[0] = nums[i];
    nums[i] = tmp;
  }
  return nums;
}
public void max_heapify(int[] nums, int f) {
  int child;
  // 遍历所有父节点
  for(int i = (f-1)/2;i>=0;i--) {
    child = i*2+1;
    if(child!=f && nums[child+1]>nums[child]) {
      child++;
    }
    // 如果父节点比最大的子节点小就交换。
    if(nums[i]<nums[child]) {
      int tmp = nums[i];
      nums[i] = nums[child];
      nums[child] = tmp;
    }
  }
}

建立堆的过程, 从length/2 一直处理到0, 时间复杂度为O(n);
调整堆的过程是沿着堆的父子节点进行调整, 执行次数为堆的深度, 时间复杂度为O(lgn);
堆排序的过程由n次第2步完成, 时间复杂度为O(nlgn).

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
𝑂(𝑛log2𝑛)O(nlog2⁡n)	𝑂(𝑛log2𝑛)O(nlog2⁡n)	𝑂(𝑛log2𝑛)O(nlog2⁡n)	𝑂(1)O(1)	不稳定

基数排序

算法描述

从最低位开始，具体算法描述如下：

取得数组中的最大数，并取得位数；
arr为原始数组，从最低位开始取每个位组成radix数组；
对radix进行计数排序（利用计数排序适用于小范围数的特点）；

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46


public int[] sortArray(int[] nums) {
        sort(nums);
        return nums;
    }
    public static void sort(int[] arr) {
    if (arr.length <= 1) return;

    //取得数组中的最大数，并取得位数
    int max = 0;
    for (int i = 0; i < arr.length; i++) {
        if (max < arr[i]) {
            max = arr[i];
        }
    }
    int maxDigit = 1;
    while (max / 10 > 0) {
        maxDigit++;
        max = max / 10;
    }
    //申请一个桶空间
    int[][] buckets = new int[10][arr.length];
    int base = 10;

    //从低位到高位，对每一位遍历，将所有元素分配到桶中
    for (int i = 0; i < maxDigit; i++) {
        int[] bktLen = new int[10];        //存储各个桶中存储元素的数量

        //分配：将所有元素分配到桶中
        for (int j = 0; j < arr.length; j++) {
            int whichBucket = (arr[j] % base) / (base / 10);
            buckets[whichBucket][bktLen[whichBucket]] = arr[j];
            bktLen[whichBucket]++;
        }

        //收集：将不同桶里数据挨个捞出来,为下一轮高位排序做准备,由于靠近桶底的元素排名靠前,因此从桶底先捞。
        // 以个位数为例，个位数越大，加入arr的时间就越迟。那么在之后判断十位数的时候，也会较迟的加入arr中，因此而产生相同十位数，个位数的不同
        int k = 0;
        for (int b = 0; b < buckets.length; b++) {
            for (int p = 0; p < bktLen[b]; p++) {
                arr[k++] = buckets[b][p];
            }
        }
        System.out.println("Sorting: " + Arrays.toString(arr));
        base *= 10;
    }
}

以下是基数排序算法复杂度，其中k为最大数的位数：

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(d*(n+r))	O(d*(n+r))	O(d*(n+r))	O(n+r)	稳定

其中，d 为位数，r 为基数，n 为原数组个数。在基数排序中，因为没有比较操作，所以在复杂上，最好的情况与最坏的情况在时间上是一致的，均为 O(d*(n + r))。

希尔排序

算法描述

选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
按增量序列个数 k，对序列进行 k 趟排序；
每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

效果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


public static void sort(int[] a) {
    int length = a.length;
    int h = 1;
    while (h < length / 3) h = 3 * h + 1;
    for (; h >= 1; h /= 3) {
        for (int i = 0; i < a.length - h; i += h) {
            for (int j = i + h; j > 0; j -= h) {
                if (a[j] < a[j - h]) {
                    int temp = a[j];
                    a[j] = a[j - h];
                    a[j - h] = temp;
                }
            }
        }
    }
}

以下是希尔排序复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度	稳定性
O(nlog2 n)	O(nlog2 n)	O(nlog2 n)	O(1)	不稳定

应用场景

**冒泡排序：**优化后的冒泡排序可用于当数据已经基本有序，且数据量较小时；
**插入排序：**若数组基本有序且数据规模较小时，选用插入排序较好；
**希尔排序：**数据量较小且基本有序时；
**选择排序：**当数据规模较小时，选择排序性能较好；
**堆排序：**堆排序适合处理数据量大的情况，数据呈流式输入时用堆排序也很方便；
**归并排序：**数据量较大且要求排序稳定时；
**快速排序：**快速排序适合处理大量数据排序时的场景；
**基数排序：**基数排序虽然时间复杂度较低，但需要满足的条件较多，如果能满足限制条件与空间需求，基数排序自然很快。
若n较小(如n≤50)，可采用直接插入或直接选择排序。
- 若序列初始状态基本有序，则直接插入和冒泡最佳，随机的快速排序也不错。插入排序对部分有序的数组很有效，所需的比较次数平均只有选择排序的一半。
- 若n较大，则应采用时间复杂度为O(nlgn)的排序方法：快速排序、堆排序或归并排序。归并排序可以处理数百万甚至更大规模的数组，但是插入和选择做不到。归并排序的主要缺点是辅助数组所使用的额外空间和n的大小成正比。
  - 快速排序是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
  - 堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况。但这两种排序都是不稳定的。
  - 若要求排序稳定，则可选用归并排序。两两归并的排序算法并不值得提倡，通常可以将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子文件，然后再两两归并之。因为直接插入排序是稳定的，所以改进后的归并排序仍是稳定的。
- 快速排序的优点是原地排序（只需要一个很小的辅助栈），但是基准的选取是个问题，对于小数组，快速排序要比插入排序慢。
- 堆排序的优点是在排序时可以将需要排序的数组本身作为堆，无需任何额外空间，与选择排序有些类似，但所需的比较要少得多，堆排序适合例如嵌入式系统或低成本移动设备中容量有限的场景。

空间复杂度最大的排序算法

堆排序 O(n+r)，r是基数。也就是10

数据结构_八大排序【网友收集】

文章目录

八大排序以及java实现

插入排序

算法描述

选择排序

算法描述

冒泡排序

算法描述

快速排序

算法描述

归并排序

算法描述

堆排序

算法描述

基数排序

算法描述

希尔排序

算法描述

应用场景