tarjan 算法
原理:
向上标记法 o(N)
倍增算法
fa[i,j] 表示从i开始,向上走 $2^j$ 步, 能走到的节点, $0<=j <= logN$
$ depth[i] $ 表示深度
哨兵: 从i 开始跳 $2^j$ 步会跳到根节点,那么 $ fa[i,j] = 0 $ 。 $depth[0] = 0$
步骤:
- 先将2个点跳到同一层
- 2个点同时往上面条, 一直跳到 最近公共祖先的下一层
- 预处理 $ o(NlogN)$
- 查询 $o(logN) $
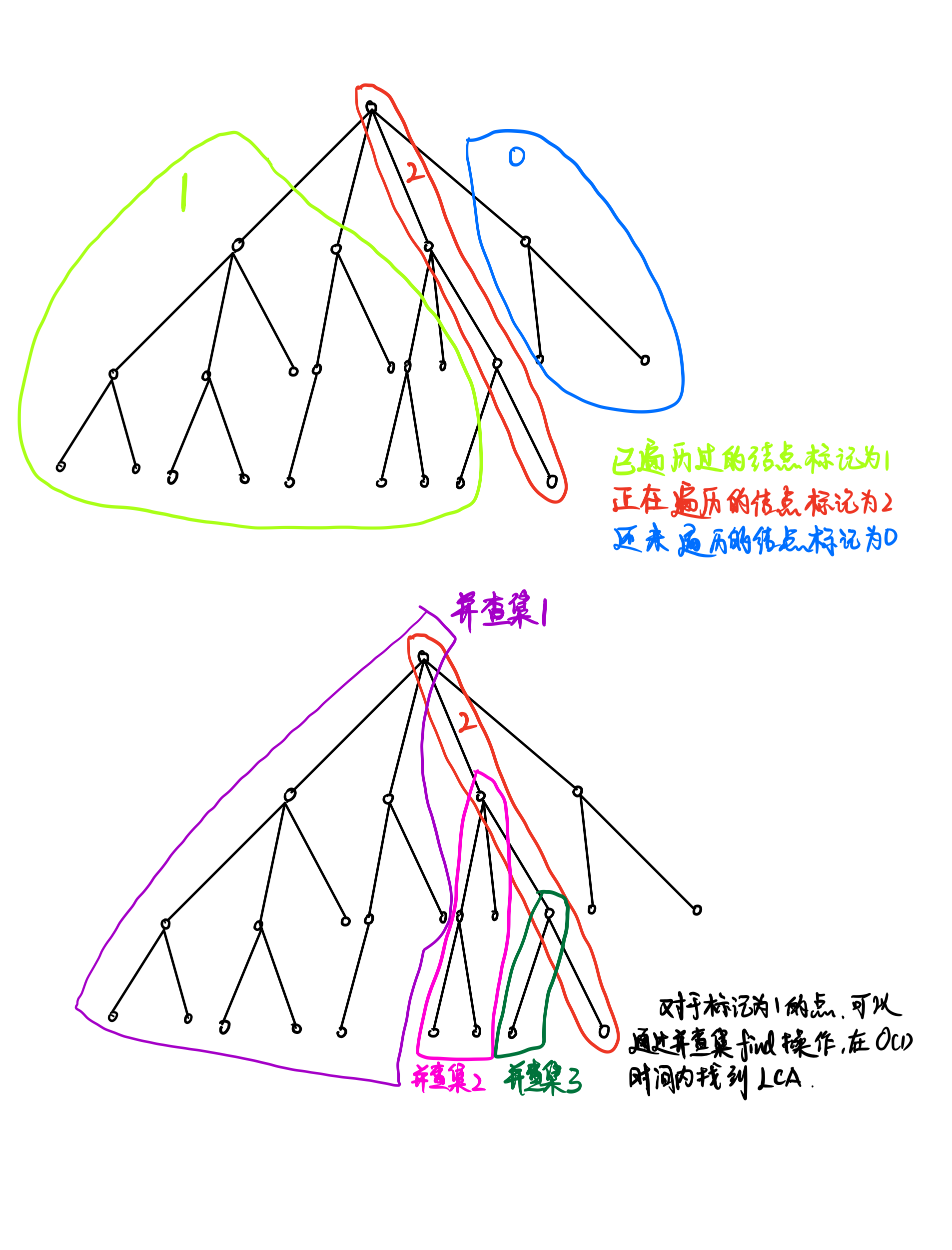
tarjan 算法原理 O(n + m)
tarjan 算法是对向上标记算法的一个优化
利用并查集 记录每个点的祖先节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
#include<bits/stdc++.h>
using namespace std;
#define next NEXT
#define x first
#define y second
#define PII pair<int,int>
unordered_map<int,vector<pair<int,int> > > tree;
int n,m;
const int MAXM = 5e5+10,MAXN = 1e5+10;
vector<pair<int,int>> query[MAXN];
int p[MAXN];
int dest[MAXM];
int find(int u) {
if (u != p[u]) p[u] = find(p[u]);
return p[u];
}
void dfs(int u,int parent) {
if (u == parent) return;
for (auto next: tree[u]) {
if (next.first == parent) continue;
//这个是相对路径的长度
dest[next.x] = dest[u] + next.y;// to_dest[x] <- u + dist[u,x]
dfs(next.x,u);
}
}
int state[MAXM];
const int Searching = 1, SearchEnd = 2;
int res[MAXN];//query 的索引问题
void tarjan(int u) {
state[u] = 1;
for(auto next: tree[u]) {
int v = next.x, w = next.y;
if(state[v] == 0) {
// state[v] = 1;
tarjan(v);
p[v] = u;//并查集 v.root = u, u是父亲节点,【可能会是最近公共祖先】
}
}
for(auto search_: query[u]) {
int v = search_.x, pos = search_.y;
if(state[v] == 2) {
//已经搜索出结果,一定是最近公共祖先
res[pos] = dest[u] + dest[v] - 2*dest[find(v)];//v是绿色部分, u 是红色部分,正在搜素
}
}
state[u] = 2;//searchENd
}
int main(void) {
cin>> n>>m;
for(int i=1;i<MAXN;++i) p[i] = i;
for( int i=0;i<n-1;++i) {
int x,y,k;
cin>> x>> y >> k;
tree[x].push_back({y,k});
tree[y].push_back({x,k});
}
for(int j=0;j<m;++j) {
int a,b;cin>> a>>b;
if (a != b) query[a].push_back({b,j} ),
query[b].push_back({a,j} );
}
dfs(1,-9);
tarjan(1);
for(int i=0;i<m;++i)
cout << res[i] <<endl;
return 0;
}
|
祖孙询问
给定一棵包含 nn 个节点的有根无向树,节点编号互不相同,但不一定是 1∼n 。
有 mm 个询问,每个询问给出了一对节点的编号 x 和 y,询问 x 与 y 的祖孙关系。
输入格式
输入第一行包括一个整数 表示节点个数;
接下来 nn 行每行一对整数 a 和 b ,表示 a 和 b 之间有一条无向边。如果 b 是 −1,那么 a 就是树的根;
第 n+2 行是一个整数 m 表示询问个数;
接下来 m 行,每行两个不同的正整数 x 和 y ,表示一个询问。
输出格式
对于每一个询问,若 x 是 y 的祖先则输出 1 ,若 y 是 x 的祖先则输出 2 ,否则输出 0。
数据范围
$1≤n,m≤4×10^4$
$1≤每个节点的编号≤4×10^4 $
输入样例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19
|
输出样例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
|
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
// #define PII pair<int,int>
typedef pair<int, int> PII;
#define query Query0
unordered_map<int,vector<int> > routes;
int depth[N];
int state[N];
int p[N];
// int fa[N][16];
// queue<int>q;
int n,m;
int Root;
int find(int x) // 并查集
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// int bfs(int root = Root) {
// memset(depth,0x3f,sizeof depth);
// memset(fa,0,sizeof fa);
// depth[0] = 0;
// depth[root] = 1;
// //入队
// q.push(root);
// while(q.size()) {
// int x = q.front();q.pop();
// for(int node: routes[x]) {
// //相邻节点
// if(depth[node] > depth[x] + 1) {
// //入队,更新其他节点
// q.push(node);
// //更新 depth 信息
// depth[node] = depth[x]+1;
// //更新父亲节点信息
// fa[node][0] = x;
// for(int i=1;i<=15;++i) {
// //初始化,父亲的父亲 【因为是从 父亲的 父亲那边走过来的,所以父亲发父亲已经初始化了】
// //用已经计算出的 解决 没有计算出的
// fa[node][i] = fa[fa[node][i-1]][i-1];
// }
// }
// }
// }
// }
// int lca(int x,int y) {
// if(depth[x]<depth[y]) swap(x,y);
// for(int i=15;i>=0;--i) {
// if(depth[fa[x][i]] >= depth[y]) {
// x = fa[x][i];
// }
// }
// if(x==y) return x;
// //b是 a的最近公共祖先
// for(int i=15;i>=0;--i) {
// if(fa[x][i]!=fa[y][i])
// x = fa[x][i] ,y =fa[y][i];
// }
// return fa[x][0];
// }
struct Info {
int u,id;
};
vector<Info> request[N];
vector<PII> query;
int res[N];
void tarjan(int u) {
state[u] = 1;
for(auto next: routes[u]) {
if(!state[next]) {
tarjan(next);
p[next] = u;
}
}
for(auto item:request[u]) {
int v = item.u,pos = item.id;
if(state[v] == 2) {
res[pos] = find(v);//v 是根节点 【最近公共祖先是 find(v) 】
}
}
state[u] = 2;
}
int main(void) {
cin>>n;
Root = 0;
for(int i=0;i<n;++i) {
int x,y;
cin>>x>>y;
if(y==-1) {
Root = x;
}else{
routes[x].push_back(y);
routes[y].push_back(x);
}
}
for(int i=1;i<N;++i) p[i] = i;
cin>> m;
for(int i=0;i<m;++i)
{
int u,v;
cin>> u>>v;
request[u].push_back({v,i});
request[v].push_back({u,i});
query.push_back({u,v});
}
// cout << Root <<endl;
tarjan(Root);
for(int i=0;i<m;++i ) {
pair<int,int> pp = query[i];
if (res[i] == pp.first) puts("1");
else if(res[i] == pp.second) puts("2");
else puts("0");
}
return 0;
}
|

